Machine Learning for Marketing in Python¶
Companies track and store tons of data on their customers and the audiences they advertise too. Data like the things customers purchase, click on, ratings, reviews, web browser cookies, social media engagement, and demographic information just to name a few.
Types of Data:
- 1st party: Data the company has collected internally from a website analytics platform or business analysis tools. Thus is the most valuable data because it provides specifics about existing customers and is a key component of ad retargeting and retention campaigns.
- 2nd party: Someone else's first part data. This is usually an arrangement with partners who are willing to share their customer data in a mutually beneficial scenario.
- 3rd party: Data that is typically purchased on a large scale from publishers and sold by companies like Peer39, eXelate and BlueKai. These companies are often called data aggregators. Their is a large volume of valuable demographic and behavioral data available from 3rd parts aggregators. This data plays a critical role in audience targeting and extension but is also available to the competition.
Once high-quality customer data is available in a consumable fashion, the next step is to identify the AI-ML use cases for the companies. Here are the most common use cases that marketers can consider in order to personalize the experience for the customer or target audience.
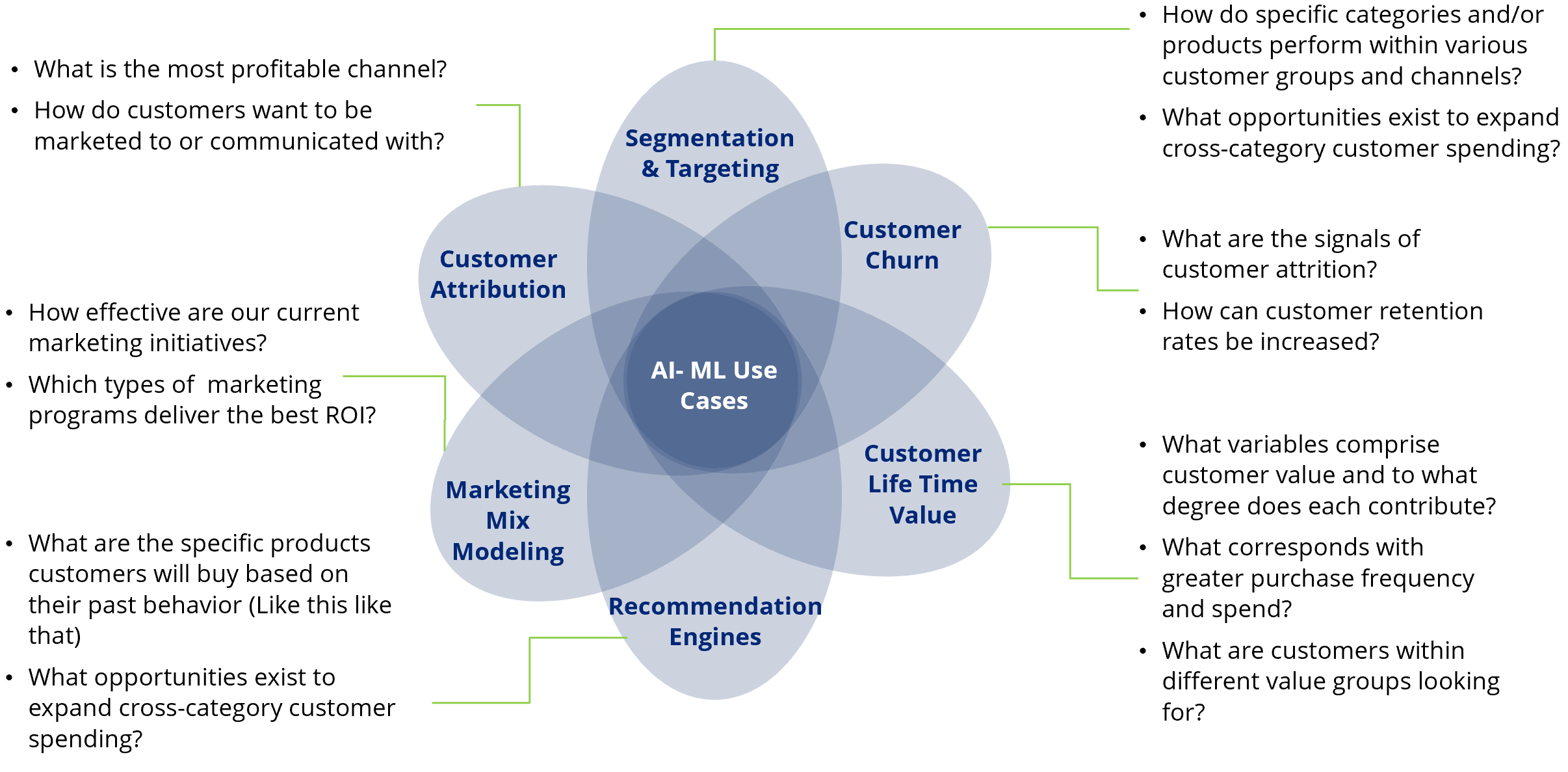
An integrated analytics strategy is the key for Chief Marketing Officers (CMO) to discover, interpret, and communicate of meaningful patterns in the data. Most organizations go through this journey to eventually implement advanced analytics that enables a high level of personalization for each customer.
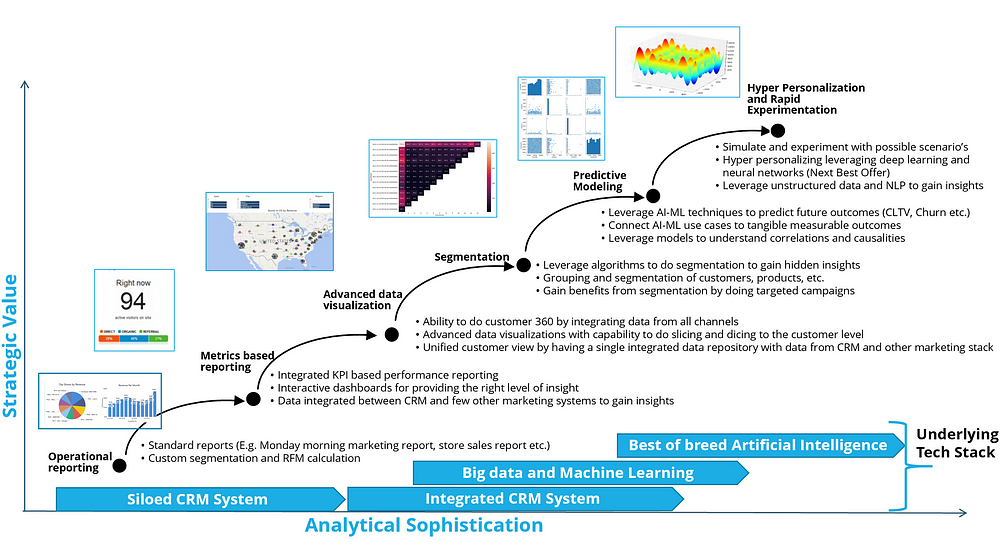
It all starts with operational reports coming out of a CRM (customer relationship management) database. CRM's are one of many different approaches that allow a company to manage and analyse its own interactions with its past, current and potential customers. It uses data analysis about customers' history with a company to improve business relationships with customers, specifically focusing on customer retention and ultimately driving sales growth.
The CRM compiles data from a range of different communication channels, including a company's website, telephone, email, live chat, marketing materials and, social media. Through the CRM approach and the systems used to facilitate it, businesses learn more about their target audiences and how to best cater for their needs.
After establishing a CRM database companies then create metrics-based reporting and eventually advanced data visualizations. Visualization tools such as Tableau, Power BI or AWS QuickSight are leaders in enterprise data visualizations.
As the organizations move towards predictive analytics and other advanced analytics, a variety of tools can be used ranging from open source tools to paid ones. The most popular open source tools are Python and R and there is a thriving community that contributes to this knowledge repository.
The underlying data foundation needs to support these use cases and many organizations are moving toward cloud data lakes and warehouses. The most popular data lake is provided by AWS and uses AWS S3 and warehouse is AWS Red Shift or DynamoDB. The cloud provides the infrastructure for having an integrated and consolidated data that enables analytics and machine learning R&D to generate insights that can be used to personalize experience for the customers.
Once the data foundation is in place and analytics use cases are implemented, a great marketing organization should set up experiments to continuously test, iterate and learn to avoid the guesswork as much as possible. The companies with sophisticated customer analytics and create more 2-way interactions with customers are the ones that are most likely to win in the long run.
Investigate the data¶
In this exercise, we will explore the key characteristics of the telecom churn dataset. Each row represents a customer, each column contains customer’s attributes described on the column Metadata.
The data set includes information about:
- Customers who left within the last month – the column is called Churn
- Services that each customer has signed up for – phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies
- Customer account information – how long they’ve been a customer, contract, payment method, paperless billing, monthly charges, and total charges
- Demographic info about customers – gender, age range, and if they have partners and dependents
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', None)
fpath = 'https://assets.datacamp.com/production/repositories/4976/datasets/252c7d50740da7988d71174d15184247463d975c/telco.csv'
telco_raw = pd.read_csv(fpath)
telco_raw.info()
telco_raw.head()
telco_raw.describe()
telco_raw.describe(include=np.object)
telco_raw.nunique()
There is something off about TotalCharges. On inspection, total charges should be numerical but yet that column is showing as a string type. Let's find out why that is the case using regex
import warnings
warnings.filterwarnings('ignore')
dec_reg_exp = r'^[+-]{0,1}((\d*\.)|\d*)\d+$'
abnormal_total_charges = telco_raw[~telco_raw.TotalCharges.str.contains(dec_reg_exp)]
abnormal_total_charges.TotalCharges
There seems to be some rows blank for the TotalCharges column
round((len(abnormal_total_charges.TotalCharges) / len(telco_raw.TotalCharges)) * 100, 2)
The TotalCharges for these observations need to be imputed or dropped. The percentage of blank values is about $0.16\%$, it is an insignificant portion of the entire dataset so let's drop these observations.
telco_raw = telco_raw[telco_raw.TotalCharges.str.contains(dec_reg_exp)]
telco_raw['TotalCharges'] = telco_raw['TotalCharges'].astype(float)
telco_raw.dtypes
Separate numerical and categorical columns¶
In the last exercise, we have explored the dataset characteristics and are ready to do some data pre-processing. We will now separate categorical and numerical variables from the telco_raw DataFrame with a customized categorical vs. numerical unique value count threshold.
# Store customerID and Churn column names
custid = ['customerID']
target = ['Churn']
# Store categorical column names
categorical = telco_raw.nunique()[telco_raw.nunique() < 5].keys().tolist()
# Remove target from the list of categorical variables
categorical.remove(target[0])
# Store numerical column names
numerical = [x for x in telco_raw.columns if x not in custid + target + categorical]
print(f'Numerical cols = {numerical}, \n\nCategorical cols = {categorical}')
Encode categorical and scale numerical variables¶
In this final step, we will perform one-hot encoding on the categorical variables and then scale the numerical columns.
from sklearn.preprocessing import StandardScaler
# Perform one-hot encoding to categorical variables
telco_raw_ohe = pd.get_dummies(data = telco_raw, columns = categorical, drop_first=True)
# Initialize StandardScaler instance
scaler = StandardScaler()
# Scale all numerical variables
for num_ft in numerical:
telco_raw_ohe[num_ft] = scaler.fit_transform(telco_raw_ohe[num_ft].values.reshape(-1, 1))
# Drop customerID and Churn
X = telco_raw_ohe.drop(['customerID', 'Churn'], axis=1)
# Create a binary target variable
target_map = {'Yes': 1, 'No': 0}
Y = telco_raw_ohe.Churn.map(target_map)
Split data to training and testing¶
We are now ready to build an end-to-end machine learning model by following a few simple steps! We will explore modeling nuances in much more detail soon, but for now we will practice and understand the key steps.
from sklearn.model_selection import train_test_split
# Split X and Y into training and testing datasets
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.25)
# Ensure training dataset has only 75% of original X data
print(train_X.shape[0] / X.shape[0])
# Ensure testing dataset has only 25% of original X data
print(test_X.shape[0] / X.shape[0])
Churn prediction fundamentals¶
What is churn?
- Churn happens when a customer stops buying / engaging
- The business context could be contractual or non-contractual
- Sometimes churn can be viewed as either voluntary or involuntary
- Voluntary: Customer decided to stop using the product or service
- Involuntary: Customer fails to automatically update their subscription due to credit card expiration or their blockers
Types of churn
Main churn typology is based on two business model types:
- Contractual (phone subscription, TV streaming subscription)
- Non-contractual (grocery shopping, online shopping)
Modeling different types of churn:
- Non-contractual churn is harder to define and model, as there's no explicit customer decision
- We will model contractual churn in the telecom business model (contractual churn)
Fit a decision tree¶
Now, we will take a stab at building a decision tree model. The decision tree is a list of machine-learned if-else rules that decide in the telecom churn case, whether customers will churn or not.
from sklearn import tree
from sklearn.metrics import accuracy_score
# Initialize the model with max_depth set at 5
mytree = tree.DecisionTreeClassifier(max_depth = 5)
# Fit the model on the training data
treemodel = mytree.fit(train_X, train_Y)
# Predict values on the testing data
pred_Y = treemodel.predict(test_X)
# Measure model performance on testing data
accuracy_score(test_Y, pred_Y)
Predict churn with decision tree¶
Now we will build a more complex decision tree with additional parameters to predict customer churn. Here we will run the decision tree classifier again on our training data, predict the churn rate on unseen (test) data, and assess model accuracy on both datasets.
# Initialize the Decision Tree
clf = tree.DecisionTreeClassifier(max_depth = 7,
criterion = 'gini',
splitter = 'best')
# Fit the model to the training data
clf = clf.fit(train_X, train_Y)
# Predict the values on test dataset
pred_Y = clf.predict(test_X)
# Print accuracy values
print("Training accuracy: ", np.round(clf.score(train_X, train_Y), 3))
print("Test accuracy: ", np.round(accuracy_score(test_Y, pred_Y), 3))
Explore churn rate and split data¶
In this lesson, we're going to dig deeper into the data preparation needed for using machine learning to perform churn prediction. We will explore the churn distribution and split the data into training and testing before we proceed to modeling. In this step we get to understand how the churn rate is distributed, and pre-process the data so we can build a model on the training set, and measure its performance on unused testing data.
telcom = telco_raw_ohe.copy()
telcom.Churn = telcom.Churn.map(target_map)
# Print the unique Churn values
print(set(telcom['Churn']))
# Calculate the ratio size of each churn group
ratio = telcom.groupby(['Churn']).size() / telcom.shape[0] * 100
print('\n', ratio)
# Import the function for splitting data to train and test
from sklearn.model_selection import train_test_split
# Split the data into train and test
train, test = train_test_split(telcom, test_size = .25)
We can see that there are over $26\%$ churned customers and over $73\%$ non churned customers. There is some calss imbalance but not severe. Typically if the minority class is less than $5\%$ then we should worry about exploring ways to increase the minority class or decrease the majority class over/under sampling techniques.
Separate features and target variable¶
Now that you have split the data intro training and testing, it's time to perform he final step before fitting the model which is to separate the features and target variables into different datasets.
# Store column names from `telcom` excluding target variable and customer ID
cols = [col for col in telcom.columns if col not in custid + target]
# Extract training features
train_X = train[cols]
# Extract training target
train_Y = train[target]
# Extract testing features
test_X = test[cols]
# Extract testing target
test_Y = test[target]
print(cols)
logistic regression¶
- Classification model for a binary target variable
- Models the logarithm of the odds ratio
- Odds ratio: The probability of an even occurring divided by the probability of the event not occurring $ \frac{p}{1-p}$
For example:
If the probability of churn is $75\%$ then the probability of no churn is $25\%$, hence the odds ratio will be $75\%$ divided by $25\%$, or $3$ the base $10$ logarithm of $3$ $log_{10}(3)$ is roughly $0.48$.
This approach helps to find the decision boundary between the 2 classes while keeping the coefficients linearly related to the target variable.
prob_churn = 0.75
prob_no_churn = 1 - 0.75
odds = prob_churn / prob_no_churn
log_odds = np.log10(odds).round(2)
print(f'Probability of churn = {prob_churn} \nProbability of no churn = {prob_no_churn} \nOdds ratio = {odds} \nLog odds = {log_odds}')
Fit logistic regression model¶
Logistic regression is a simple yet very powerful classification model that is used in many different use cases. We will now fit a logistic regression on the training part of the telecom churn dataset, and then predict labels on the unseen test set. Afterwards, we will calculate the accuracy of our model predictions.
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
# Fit logistic regression on training data
logreg.fit(train_X, train_Y)
# Predict churn labels on testing data
pred_test_Y = logreg.predict(test_X)
# Calculate accuracy score on testing data
test_accuracy = accuracy_score(test_Y, pred_test_Y)
# Print test accuracy score rounded to 4 decimals
print('Test accuracy:', round(test_accuracy, 4))
Fit logistic regression with L1 regularization¶
We will now run a logistic regression model on scaled data with L1 regularization to perform feature selection alongside model building. Different C values have an effect on your accuracy score and the number of non-zero features. In this exercise, we will set the $C$ value to $0.025$.
# Initialize logistic regression instance
logreg = LogisticRegression(penalty='l1', C=0.025, solver='liblinear')
# Fit the model on training data
logreg.fit(train_X, train_Y)
# Predict churn values on test data
pred_test_Y = logreg.predict(test_X)
# Print the accuracy score on test data
print('Test accuracy:', round(accuracy_score(test_Y, pred_test_Y), 4))
Identify optimal L1 penalty coefficient¶
We will now tune the $C$ parameter for the L1 regularization to discover the one which reduces model complexity while still maintaining good model performance metrics. We will run a for loop through possible $C$ values and build logistic regression instances on each, as well as calculate performance metrics.
from sklearn.metrics import recall_score
C = [1, 0.5, 0.25, 0.1, 0.05, 0.025, 0.01, 0.005, 0.0025]
l1_metrics = np.empty((len(C),3), float)
# Run a for loop over the range of C list length
for index in range(0, len(C)):
# Initialize and fit Logistic Regression with the C candidate
logreg = LogisticRegression(penalty='l1', C=C[index], solver='liblinear')
logreg.fit(train_X, train_Y)
# Predict churn on the testing data
pred_test_Y = logreg.predict(test_X)
# Create non-zero count and recall score columns
l1_metrics[index,0] = C[index]
l1_metrics[index,1] = np.count_nonzero(logreg.coef_)
l1_metrics[index,2] = recall_score(test_Y, pred_test_Y)
# Name the columns and print the array as pandas DataFrame
col_names = ['C','Non-Zero Coeffs','Recall']
np.set_printoptions(suppress=True)
pd.DataFrame(l1_metrics, columns=col_names)
We can now explore the $C$ values and associated count of non-zero coefficients and the recall score to decide which parameter value to choose.
Fit decision tree model¶
Now we will fit a decision tree on the training set of the telecom dataset, and then predict labels on the unseen testing data, and calculate the accuracy of our model predictions. We will see the difference in the performance compared to the logistic regression.
# Initialize decision tree classifier
mytree = tree.DecisionTreeClassifier()
# Fit the decision tree on training data
mytree.fit(train_X, train_Y)
# Predict churn labels on testing data
pred_test_Y = mytree.predict(test_X)
# Calculate accuracy score on testing data
test_accuracy = accuracy_score(test_Y, pred_test_Y)
# Print test accuracy
print('Test accuracy:', round(test_accuracy, 4))
Identify optimal tree depth¶
Now we will tune the max_depth parameter of the decision tree to discover the one which reduces over-fitting while still maintaining good model performance metrics. We will run a for loop through multiple max_depth parameter values and fit a decision tree for each, and then calculate performance metrics.
depth_list = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
depth_tuning = np.empty((len(depth_list),2), float)
# Run a for loop over the range of depth list length
for index in range(0, len(depth_list)):
# Initialize and fit decision tree with the `max_depth` candidate
mytree = tree.DecisionTreeClassifier(max_depth=depth_list[index])
mytree.fit(train_X, train_Y)
# Predict churn on the testing data
pred_test_Y = mytree.predict(test_X)
# Calculate the recall score
depth_tuning[index,0] = depth_list[index]
depth_tuning[index,1] = recall_score(test_Y, pred_test_Y)
# Name the columns and print the array as pandas DataFrame
col_names = ['Max_Depth','Recall']
pd.DataFrame(depth_tuning, columns=col_names)
You can see how the recall scores change with different depth parameter values, and can make a decision on which one to choose.
Plot feature importances¶
Here, we will extract and plot the feature importances from a fitted decision tree model.
import matplotlib.pyplot as plt
import matplotlib.cm as cm
mytree = tree.DecisionTreeClassifier(max_depth=10)
mytree.fit(train_X, train_Y)
feature_names = train_X.columns
# Get feature importances from our random forest model
importances = mytree.feature_importances_
# Get the index of importances from greatest importance to least
sorted_index = np.argsort(-importances)[::-1]
x = range(len(importances))
# Create tick labels
labels = np.array(feature_names)[sorted_index]
plt.figure(figsize=(10, 8))
colors = colors = cm.rainbow(np.linspace(0, 1, len(feature_names)))
plt.barh(x, importances[sorted_index], tick_label=labels, color=colors);
Explore logistic regression coefficients¶
The coefficients can be interpreted as the change in log odds of the target variable associated with $1$ unit increase in the the input feature value.
For example if the input feature is tenure in years then, increase in tenure by one year will have an effect equal to the coefficient to the log odds.
The coefficients of the model output are in the log odds scale which is difficult to interpret.
The solution is to calculate the exponent of the coefficients, which will give us the change in the actual odds associated with a $1$ unit increase in the feature value
We will now explore the coefficients of the logistic regression to understand what is driving churn to go up or down. For this exercise, we will extract the logistic regression coefficients from our fitted model, and calculate their exponent to make them more interpretable.
logreg = LogisticRegression()
# Fit logistic regression on training data
logreg.fit(train_X, train_Y)
# Predict churn labels on testing data
pred_test_Y = logreg.predict(test_X)
# Combine feature names and coefficients into pandas DataFrame
feature_names = pd.DataFrame(train_X.columns, columns=['Feature'])
log_coef = pd.DataFrame(np.transpose(logreg.coef_), columns=['Coefficient'])
coefficients = pd.concat([feature_names, log_coef], axis = 1)
# Calculate exponent of the logistic regression coefficients
coefficients['Odds_ratio'] = np.exp(coefficients['Coefficient'])
coefficients['Probability'] = coefficients['Odds_ratio'] / (1 + coefficients['Odds_ratio'])
coefficients['Pct_odds_increase'] = round((coefficients['Odds_ratio'] - 1)*100)
# Remove coefficients that are equal to zero
coefficients = coefficients[coefficients['Coefficient']!=0]
# Print the values sorted by the exponent coefficient
coefficients.sort_values(by=['Odds_ratio'], ascending=False)
Values $< 1$ decrease the odds values $> 1$ increase the odds
So the effect of $1$ additional year of tenure decrease the odds of churn by $1 - 0.283$. This translates to roughly a $72\%$ decrease in churn odds
We have extracted and transformed logistic regression coefficients and can now understand which of them increase or decrease the odds of churn!
Break down decision tree rules¶
In this exercise we will extract the if-else rules from the decision tree and plot them to identify the main drivers of the churn.
import pydotplus
#import graphviz
from IPython.display import Image
# Export graphviz object from the trained decision tree
exported = tree.export_graphviz(decision_tree=mytree,
# Assign feature names
out_file=None, feature_names=train_X.columns,
max_depth=2,
# Set precision to 1 and add class names
precision=1, class_names=['Not churn','Churn'], filled = True)
# Draw graph
graph = pydotplus.graph_from_dot_data(exported)
# Show graph
Image(graph.create_png())
Customer Lifetime Value (CLV) basics¶
CLV is a measurement of how valuable a customer is to your company, not just on a purchase-by-purchase basis but across the whole relationship.
CLV is the total worth to a business of a customer over the whole period of their relationship. It’s an important metric as it costs less to keep existing customers than it does to acquire new ones, so increasing the value of your existing customers is a great way to drive growth.
Knowing the CLV helps businesses develop strategies to acquire new customers and retain existing ones while maintaining profit margins. CLV represents an upper limit on spending to acquire new customers. For this reason it is an important element in calculating payback of advertising spent in market mix modeling.
- Measurement of customer value
- Can be historical or predicted
- Multiple approaches, depends on business type
- Some methods are formula-based, some are predictive and distribution based
Basic income, profitability and customer metrics
- Revenue: the income generated from normal business operations and includes discounts and deductions for returned merchandise. It is the top line or gross income figure from which costs are subtracted to determine net income.
- Profit margin: Represents what percentage of sales has turned into profits. Simply put, the percentage figure indicates how many cents of profit the business has generated for each dollar of sale. For instance, if a business reports that it achieved a $35\%$ profit margin during the last quarter, it means that it had a net income of $\$0.35$ for each dollar of sales generated.
- Customer retention rate (CRR): A measure of the number of customers that a company continues to do business with over a given period of time. Customer retention rate is expressed as a percentage of a company’s existing customers that maintain loyalty to the business in that window. Customer retention focuses on loyalty and is the inverse of churn metrics.
where
- $E$ is the number of customers at the end of a period
- $N$ is the number of new customers acquired during that period
- $S$ is the number of customers at the start of that period
- Churn rate: Is the rate at which customers stop doing business with an entity. It is most commonly expressed as the percentage of customers who discontinue their subscriptions/service with a company within a given time period. For a company to expand its clientele, its growth rate (measured by the number of new customers) must exceed its churn rate.
Historical CLV¶
- Sum revenue of all past transactions
- Multiply by the profit margin
- Alternatively - sum profit of all past transactions, if available
- Challenge 1 - does not account for tenure, retention and churn
- Challenge 2 - does not account for new customers and their future revenue
Basic CLV formula¶
- Multiply average revenue with profit margin to get average profit
- Multiply it with average customer lifespan
Granular CLV formula¶
- Multiply average revenue per purchase with average frequency and with profit margin
- Multiply it with average customer lifespan
- Accounts for both average revenue per transaction and average frequency per period
Traditional CLV formula¶
- Multiply average revenue with profit margin
- Multiple average profit with the retention to churn rate
- Churn can be derived from retention and equals $1$ minus retention rate
- Accounts for customer loyalty, most popular approach
- The retention to churn ratio $\frac{\text{Retention Rate}}{\text{Churn Rate}}$ gives a multiplier that acts as a proxy to the expected length of the customer lifespan within the company. It also assumes churn is final, therefore the timeframe used for the retention and churn is critical. Especially, in a non-contractual business setting, you need to make sure customers who are defined as chrned within this timeframe do not return later.
Online retail dataset¶
This dataset contains transactions from a retailer with variables on money spent, quantity and other values for each transaction.
The cohorts dataset derived from online retail dataset is created by assigning each customer to a monthly cohort, based on the month they made their first purchase. Then a pivot table is created with the activity counts for each cohort in the subsequent months.
This means that in each row we have the same group of customers who started buying on month one, and then some of them return in the subsequent months while, others don't. We will use it to calculate retention rate.
cohort_counts = pd.read_csv('cohort_counts.csv').reset_index().set_index('CohortMonth',
drop=True).drop('index', axis=1)
cohort_counts
Build retention and churn tables¶
We have learned the main elements of the customer lifetime value calculation and certain variations of it. Now we will use use the monthly cohort activity dataset to calculate retention and churn values, which we will then explore and later use to project average customer lifetime value.
import seaborn as sns
# Extract cohort sizes from the first column of cohort_counts
cohort_sizes = cohort_counts.iloc[:,0]
# Calculate retention table by dividing the counts with the cohort sizes
retention = cohort_counts.divide(cohort_sizes, axis=0)
# Calculate churn table
churn = 1 - retention
# Print the retention table
plt.figure(figsize=(12,6))
sns.heatmap(retention, annot=True, fmt=".2f", annot_kws={"size": 12})
plt.yticks(rotation=0)
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()
We are now ready to explore retention and churn rates.
Explore retention and churn¶
Now that we have calculated the monthly retention and churn metrics for monthly customer cohorts, we can calculate the overall mean retention and churn rates. We will use the .mean() method twice in a row (this is called "chaining") to calculate the overall mean. We will have to exclude the first month values (first column) from this calculation as they are constant given this is the first month the customers have been active therefore their retention will be $100\%$ and churn will be $0\%$ for all cohorts.
# Calculate the mean retention rate
retention_rate = retention.iloc[:,1:].mean().mean()
# Calculate the mean churn rate
churn_rate = churn.iloc[:,1:].mean().mean()
# Print rounded retention and churn rates
print('Retention rate: {:.2f}; Churn rate: {:.2f}'.format(retention_rate, churn_rate))
Exploring these rates is critical in customer lifetime value calculation as it gives you insight into the customer behavior.
The goal of CLV¶
- Measure customer value in revenue / profit
- Benchmark customers
- Identify maximum investment into customer acquisition
- In our case - we'll skip the profit margin for simplicity and use revenue-based CLV formulas
Calculate basic CLV¶
We are now ready to calculate average customer lifetime with three different methods! In this exercise we will calculate the basic CLV which multiplies average monthly spent with the projected customer lifespan.
import datetime as dt
# Define a function that will parse the date
def get_day(x):
return dt.datetime(x.year, x.month, x.day)
online = pd.read_csv('online.csv', index_col='Unnamed: 0')
online.InvoiceDate = pd.to_datetime(online.InvoiceDate)
online['InvoiceDay'] = online['InvoiceDate'].apply(get_day)
grouping = online.groupby('CustomerID')['InvoiceDay']
online['InvoiceMonth'] = online['InvoiceDate'].dt.to_period('M')
online['TotalSum'] = online['UnitPrice'] * online['Quantity']
online.head()
# Calculate monthly spend per customer
monthly_revenue = online.groupby(['CustomerID','InvoiceMonth'])['TotalSum'].sum()
# Calculate average monthly spend
monthly_revenue = np.mean(monthly_revenue)
# Define lifespan to 36 months
lifespan_months = 36
# Calculate basic CLV
clv_basic = monthly_revenue * lifespan_months
# Print basic CLV value
print('Average basic CLV is {:.1f} USD'.format(clv_basic))
Calculate granular CLV¶
In this scenario we will use more granular data points at the invoice level. This approach uses more granular data and can give a better customer lifetime value estimate.
# Calculate average revenue per invoice
revenue_per_purchase = online.groupby(['InvoiceNo'])['TotalSum'].mean().mean()
# Calculate average number of unique invoices per customer per month
frequency_per_month = online.groupby(['CustomerID','InvoiceMonth'])['InvoiceNo'].nunique().mean()
# Define lifespan to 36 months
lifespan_months = 36
# Calculate granular CLV
clv_granular = revenue_per_purchase * frequency_per_month * lifespan_months
# Print granular CLV value
print('Average granular CLV is {:.1f} USD'.format(clv_granular))
You can see how the granular approach gets us a different lifetime value estimate than the basic one.
Calculate traditional CLV¶
Now we will calculate one of the most popular descriptive CLV models that accounts for the retention and churn rates. This gives a more robust estimate, but comes with certain assumptions that have to be validated.
# Calculate monthly spend per customer
monthly_revenue = online.groupby(['CustomerID','InvoiceMonth'])['TotalSum'].sum().mean()
# Calculate average monthly retention rate
retention_rate = retention.iloc[:,1:].mean().mean()
# Calculate average monthly churn rate
churn_rate = 1 - retention_rate
# Calculate traditional CLV
clv_traditional = monthly_revenue * (retention_rate / churn_rate)
# Print traditional CLV and the retention rate values
print('Average traditional CLV is {:.1f} USD at {:.1f} % retention_rate'.format(clv_traditional,
retention_rate*100))
As you can see, the traditional CLV formula yields a much lower estimate as it accounts for monthly retention which is quite low for this company.
Predicting customers next month purchases¶
We will be using regression because our target variable we are predicting is continuous.
We will use recency, frequency, monetary (RFM) features
- RFM - approach underlies many feature engineering methods
- Recency: time since last customer transaction
- Frequency: number of purchases in the observed period
- Monetary value: total amount spent in the observed period
Build features¶
We are now fully equipped to build recency, frequency, monetary value and other customer level features for our regression model. Feature engineering is the most important step in the machine learning process. In this exercise we will create five customer-level features that we will then use in predicting next month's customer transactions. These features capture highly predictive customer behavior patterns.
# Exclude target variable
online_X = online[online['InvoiceMonth']!='2011-11']
# Define the snapshot date
NOW = dt.datetime(2011,11,1)
# Calculate recency by subtracting current date from the latest InvoiceDate
features = online_X.groupby('CustomerID').agg({
# Calculate recency by subtracting the InvoiceDate from the snapshot date
'InvoiceDate': lambda x: (NOW - x.max()).days,
# Calculate frequency by counting unique number of invoices
'InvoiceNo': pd.Series.nunique,
# Calculate monetary value by summing all spend values
'TotalSum': np.sum,
# Calculate average and total quantity
'Quantity': ['mean', 'sum']}).reset_index()
# Rename the columns
features.columns = ['CustomerID', 'recency', 'frequency', 'monetary', 'quantity_avg', 'quantity_total']
features.head()
Define target variable¶
Here, we'll build a pandas pivot table with customers as rows, invoice months as columns, and number of invoice counts as values. We will use the last month's value as the target variable. The remaining variables can be used as the so-called lagged features in the model.
# Build a pivot table counting invoices for each customer monthly
cust_month_tx = pd.pivot_table(data=online, values='InvoiceNo',
index=['CustomerID'], columns=['InvoiceMonth'],
aggfunc=pd.Series.nunique, fill_value=0)
cust_month_tx = cust_month_tx[cust_month_tx.index.isin(features.CustomerID.unique())]
cust_month_tx.head()
# Store November 2011 sales data column name as a list
target = '2011-11'
# Store target value as `Y`
Y = cust_month_tx[target]
to_drop = cust_month_tx.columns[len(cust_month_tx.columns) - 2:]
m_lags = cust_month_tx.drop(to_drop, axis=1).reset_index()
features_lagged = pd.merge(features, m_lags, on='CustomerID')
features_lagged.info()
features_lagged.head()
Now with the target variable defined and the features built previously, we are ready to split the data into training and testing.
# Store customer identifier column name as a list
custid = ['CustomerID']
# Select feature column names excluding customer identifier
cols = [col for col in features_lagged.columns if col not in custid]
# Extract the features as `X`
X = features_lagged[cols]
# Split data to training and testing
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.25, random_state=99)
The data is now fully prepared to be used for predicting next month transactions.
Predict next month transactions¶
We are finally in the stage of predicting next month's transaction with linear regression. Here we will use the input features we've previously built, train the model on them and the target variable, and predict the values on the unseen testing data.
from sklearn.linear_model import LinearRegression
# Initialize linear regression instance
linreg = LinearRegression()
# Fit the model to training dataset
linreg.fit(train_X, train_Y)
# Predict the target variable for training data
train_pred_Y = linreg.predict(train_X)
# Predict the target variable for testing data
test_pred_Y = linreg.predict(test_X)
We have built the model on the training data, and predicted values on testing data. Next, you will explore model fit.
Measure model fit¶
Now we will measure the regression performance on both training and testing data with two metrics - root mean squared error and mean absolute error. This is a critical step where we are measuring how "close" are the model predictions compared to actual values.
from sklearn.metrics import mean_squared_error, mean_absolute_error
# Calculate root mean squared error on training data
rmse_train = np.sqrt(mean_squared_error(train_Y, train_pred_Y))
# Calculate mean absolute error on training data
mae_train = mean_absolute_error(train_Y, train_pred_Y)
# Calculate root mean squared error on testing data
rmse_test = np.sqrt(mean_squared_error(test_Y, test_pred_Y))
# Calculate mean absolute error on testing data
mae_test = mean_absolute_error(test_Y, test_pred_Y)
# Print the performance metrics
print('RMSE train: {}; RMSE test: {}\nMAE train: {}, MAE test: {}'.format(rmse_train, rmse_test,
mae_train, mae_test))
import scipy.stats as stats
import warnings
warnings.filterwarnings('ignore')
graph = sns.jointplot(x=test_Y.values, y=test_pred_Y, color='r', kind='reg')
graph.x = test_Y.values
graph.y = test_pred_Y
graph.plot_joint(plt.scatter, c='b', s=50)
graph.annotate(stats.pearsonr)
plt.xlabel('y_true')
plt.ylabel('y_pred');
Explore model coefficients¶
We will now explore the model performance from a different angle, and only on the training data. One thing you learned in the latest lesson is that not all model coefficients are statistically significant and we should look at the model summary table to explore their significance. Fortunately, the statsmodels library provides this functionality. Once you print the model summary table, explore which variables have the p-value lower than $0.05$ (i.e. lower than $5\%$) to make sure the coefficient is significant.
# Import `statsmodels.api`
import statsmodels.api as sm
# Initialize model instance on the training data
olsreg = sm.OLS(train_Y.values, train_X.values)
olsreg.exog_names[:] = list(train_X.columns)
# Fit the model
olsreg = olsreg.fit()
# Print model summary
print(olsreg.summary())
Customer and product segmentation basics¶
We will build meaningful customer segments based on their product purchases.
We will use a wholesale dataset with customer transactions.
- This is a customer by product purchase matrix, that has purchase data for each customer at a product level.
We will use unsupervised learning models. Here are some of the more popular models:
- Hierarchical clustering
- K-means
- Non-negative matrix factorization (NMF)
- Biclustering
- Gaussian mixture models (GMM)
- And many more
Explore customer product purchase dataset¶
We are now ready to plot some exploratory charts to understand the distribution of the variables and relationships between them. Here, we will explore the wholesale dataset and plot the pairwise relationships as well as the estimated distributions for each variable with the pairplot function from the seaborn library. It's an important step to explore the distribution types, and the relationships between the variables to inform the need for further data preprocessing.
fpath = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00292/Wholesale%20customers%20data.csv'
wholesale = pd.read_csv(fpath).drop(['Channel', 'Region'], axis=1)
# Print the header of the `wholesale` dataset
wholesale.head()
import seaborn as sns
# Plot the pairwise relationships between the variables
sns.pairplot(wholesale, diag_kind='kde')
# Display the chart
plt.show()
Understand differences in variables¶
Now, we will analyze the averages and standard deviations of each variable by plotting them in a barplot. This is a complementary step to the one before, as we will visually explore the differences in variable scales and variances.
# Get the statistics
averages = wholesale.mean()
std_devs = wholesale.std()
# Create column names list and same length integer list
x_names = wholesale.columns
x_ix = np.arange(wholesale.shape[1])
# Plot the averages data in gray and standard deviations in orange
plt.bar(x=x_ix-0.2, height=averages, color='grey', label='Average', width=0.4)
plt.bar(x=x_ix+0.2, height=std_devs, color='orange', label='Standard Deviation', width=0.4)
# Add x-axis labels and rotate
plt.xticks(ticks=x_ix, labels=x_names, rotation=90)
# Add the legend and display the chart
plt.legend()
plt.show()
This plot gives us a visual sense of the differences in averages and standard deviations.
Unskew the variables¶
We will now transform the wholesale columns using Box-Cox transformation, and then explore the pairwise relationships plot to make sure the skewness of the distributions has been reduced to make them more normal. This is a critical step to make sure the K-means algorithm converges and discovers homogeneous groups (a.k.a. clusters or segments) of observations.
from scipy import stats
# Define custom Box Cox transformation function
def boxcox_df(x):
x_boxcox, _ = stats.boxcox(x)
return x_boxcox
# Apply the function to the `wholesale` dataset
wholesale_boxcox = wholesale.apply(boxcox_df, axis=0)
# Plot the pairwise relationships between the transformed variables
sns.pairplot(wholesale_boxcox, diag_kind='kde')
# Display the chart
plt.show()
By using Box-Cox transformation we have successfully unskewed the variables and they now are almost normally distributed.
Normalize the variables¶
Now, for the last step in data preparation. We will transform the unskewed dataset wholesale_boxcox to the same scale, meaning all columns have a mean of $0$, and standard deviation of $1$. We will use the StandardScaler function from the sklearn.preprocessing module.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# Fit the initialized `scaler` instance on the Box-Cox transformed dataset
scaler.fit(wholesale_boxcox)
# Transform and store the scaled dataset as `wholesale_scaled`
wholesale_scaled = scaler.transform(wholesale_boxcox)
# Create a `pandas` DataFrame from the scaled dataset
wholesale_scaled_df = pd.DataFrame(data=wholesale_scaled,
index=wholesale_boxcox.index,
columns=wholesale_boxcox.columns)
# Print the mean and standard deviation for all columns
wholesale_scaled_df.agg(['mean','std']).round()
As you can see, the averages are roughly zero, and the standard deviations are around one.
Determine the optimal number of clusters¶
Here, we will use the elbow criterion method to identify the optimal number of clusters where the squared sum of error decrease becomes marginal. This is an important step to get a mathematical ball-park number of clusters to start testing. We will iterate through multiple $k$ number of clusters and run a KMeans algorithm for each, then plot the errors against each $k$ to identify the "elbow" where the decrease in errors slows downs.
from sklearn.cluster import KMeans
# Create empty sse dictionary
sse = {}
# Fit KMeans algorithm on k values between 1 and 11
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, random_state=333)
kmeans.fit(wholesale_scaled_df)
sse[k] = kmeans.inertia_
# Add the title to the plot
plt.title('Elbow criterion method chart')
# Create and display a scatter plot
sns.pointplot(x=list(sse.keys()), y=list(sse.values()))
plt.show()
You can see that the "elbow" is somewhere around $2$ or $3$ clusters, which means you should start cluster with $+1$ number of clusters i.e. with $3$ or $4$.
Build segmentation with k-means clustering¶
In this exercise, we will build the customer segmentation with KMeans algorithm. As you've identified in the previous step, the mathematically optimal number of clusters is somewhere around $3$ and $4$. Here, we will build one with $3$ segments.
# Initialize `KMeans` with 3 clusters
kmeans=KMeans(n_clusters=3, random_state=123)
# Fit the model on the pre-processed dataset
kmeans.fit(wholesale_scaled_df)
# Assign the generated labels to a new column
wholesale_kmeans4 = wholesale.assign(segment = kmeans.labels_)
wholesale_kmeans4.head()
We have created a 3-segment solution with K-means clustering and have assigned labels the the original dataset.
Alternative segmentation with NMF¶
In this exercise, we will analyze product purchase data and identify meaningful segments using non-negative matrix factorization algorithm (NMF). It works well with sparse customer by product matrices that are typical in the e-commerce or retail space. Finally, we will extract the components that we will then explore in the upcoming exercise.
# Import the non-negative matrix factorization module
from sklearn.decomposition import NMF
# Initialize NMF instance with 3 components
nmf = NMF(3)
# Fit the model on the wholesale sales data
nmf.fit(wholesale)
# Extract the components
components = pd.DataFrame(data=nmf.components_, columns=wholesale.columns)
components.head()
Visualize and interpret segmentation solutions¶
Explore the results and choose one with most business relevance (Can you name the segments? Are they ambiguous / overlapping?)
Methods to explore segments¶
- Calculate average / median / other percentile values for each variable by segment
- Calculate relative importance for each variable by segment
- We can explore the data table or plot it (heatmap is a good choice)
K-means segmentation averages¶
In this exercise, we will explore the average column values for a 3-segment solution with K-means. As part of the test & learn exploration process, visually inspecting the segmentation solutions is critical to identify the most business relevant option.
# Group by the segment label and calculate average column values
kmeans4_averages = wholesale_kmeans4.groupby(['segment']).mean().round(0)
# Print the average column values per each segment
print(kmeans4_averages)
# Create a heatmap on the average column values per each segment
sns.heatmap(kmeans4_averages.T, cmap='YlGnBu', annot=True, fmt=".1f", annot_kws={"size": 12})
plt.yticks(rotation=0)
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()
You can see how different are the 3 segments from each other - can you try to name each segment by their purchase patters?
NMF segmentation averages¶
Finally, we will visually explore the average values of the 3-segment solution built by NMF and can compare it to the K-means one. Here we will extract the features matrix $W$ which we will use to extract the hard segment assignment by choosing the column value (segment) with highest associated value in this matrix for each customer.
# Create the W matrix
W = pd.DataFrame(data=nmf.transform(wholesale), columns=components.index)
W.index = wholesale.index
W.head()
# Assign the column name where the corresponding value is the largest
wholesale_nmf3 = wholesale.assign(segment = W.idxmax(axis=1))
wholesale_nmf3.head()
# Calculate the average column values per each segment
nmf3_averages = wholesale_nmf3.groupby('segment').mean().round(0)
# Print the average column values per each segment
print(nmf3_averages)
# Plot the average values as heatmap
sns.heatmap(nmf3_averages.T, cmap='YlGnBu', annot=True, fmt=".1f", annot_kws={"size": 12})
plt.yticks(rotation=0)
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.show()